

In your case : ( f ∘ g ) ( x ) = ln (x+1 ), f ( x ) = ln ( x ) and g ( x ) =x+1. Edit: I interpreted the post to mean log base y, others might have interpreted differently. We can use the chain rule here, naming u = 2 x and remembering that the chain rule states thatĭ y/ d x = 1/ u ⋅ 2 =( 1/ 2 x) ⋅ 2 = 1/ x Derivative of ln(x+1)
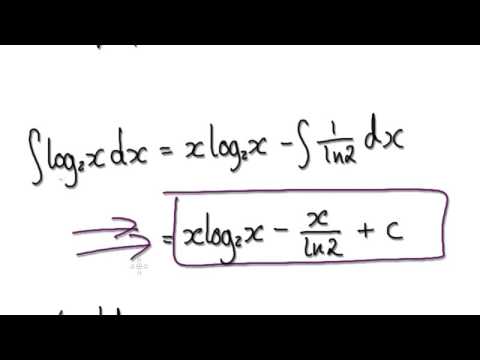
Since f ‘ ( x ) = 1/ x and g ‘ ( x ) = 2, we have : In your case : ( f ∘ g ) ( x ) = ln ( 2 x ), f ( x ) = ln ( x ) and g ( x ) = 2 x. Explanation: Before differentiating we need to change the log to base e. I can use the sum rule and constant multiple rule. Here, the interesting thing is that we have ln in the derivative of log x. This is the derivative of 100 minus 3 log x. The derivative of log x (log x with base a) is 1/(x ln a). Remember, when you see log, and the base isn't written, it's assumed to be the common log, so base 10 log. We have proven the following theorem The derivative of ln(2x) Let's find the derivative of 100 minus 3 log x. A logarithm with base 10 is called a common logarithm, and it is expressed as log ( x ). Determine if V (t) t et V ( t) t e t is increasing or decreasing at the following points. Find the tangent line to f (x) 7x +4ex f ( x) 7 x + 4 e x at x 0 x 0. For problems 1 6 differentiate the given function. Now implicitly take the derivative of both sides with respect to x remembering to multiply by dy/dx on the left-hand side since it is given in terms of y, not x.įrom the inverse definition, we can substitute x in for e^y to get Second of four videos for the Year 12 Advanced topic: Further Differentiation.All resources can be found here. When the logarithmic function is given by: f ( x) log b ( x) The derivative of the logarithmic function is given by: f ' ( x) 1 / ( x ln ( b) ) x is the function argument. Section 3-6 : Derivatives of Exponential and Logarithm Functions. Our task is to determine what is the derivative of the natural logarithm.


 0 kommentar(er)
0 kommentar(er)
